Algoritma 2 : Array Dua Dimensi Beserta Contoh Program Pascal
ilmuit.id - Setelah belajar array 1 dimensi kita lanjut ke pembahasan tentang array dua dimensi, pada algoritma 2 ini dimana penerapan algoritma mengggunakan bahasa pemrograman pascal. jika masih belum paham pascal anda bisa membacanya melalui link di bawah ini
Baca Juga : Tutorial Pemrograman Pascal Dasar
Dimana pengertian array dua dimensi menurut para pakar adalah sebagai berikut :
Raharjo ( 2010:140 ) "array dua dimensi adalah array yang memiliki dua buah elemen bertipe array, dengan kata lain array dua dimensi mempunyai subskrip yang biasanya di presentasikan dengan baris dan kolom"
Ramadhani ( 2015: 59 ) "array dimensi dua sering di analogikan sebagai sebuah matrik jika array dimensi satu hanya terdiri atas satu baris dan banyak kolom, array diemnsi dua terdiri dari banyak baris dan banyak kolom yang bertipe sama"
Baca Juga : Algoritma 2 : Pembahasan Tentang Larik / Array 1 dimensi
Perbedaan antara array 1 dimensi dan array 2 dimensi
Array 1 dimensi terdiri dari satu baris dan banyak kolom, Sedangkan array 2 dimensi terdiri dari banyak baris dan banyak kolom jika di presentasikan secara visual maka kita dapat melihat array dua dimensi seperti di bawah ini
Misalkan di contohkan secara visual :
Dari gambar 1 diatas dicontohkan array 2 dimensi mempunyai 3 baris dan 4 kolom ini hanyalah contoh jika mempresentasikan array 2 dimensi secara visual dan nilai data yang di dalamnya, hanya contoh jika nilai array sudah di input. jika belum di input maka datanya null agar kita mudah untuk memahaminya.
Maka jika ada baris kode matrik / array dua dimensi seperti ini menggunakan bahasa pasca
var data : array [ 1..50, 1..100 ] of integer ;
Maka berarti anda telah menyiapkan 50 baris dan 100 kolom di memori. indeks pertama di tunjukan oleh angka 1..50 dan indeks kedua di tunjukan oleh angka 1..100.
Tanda ( , ) pada [ 1..50 , 1..100 ] untuk memisahkan indeks pertama dan indeks kedua.
Contoh lainya :
var
Nilai_mhs : array [1..100,1..3] of Integer;
Maka jika di repsentasikan secara visual dengan gambar akan seperti di bawah ini
Array juga dapat dikombinasaikan dengan perulangan while, for dan repeat until.
Var namaarray : array [ 1..5,1..10] of integer ;
Menggunakan kata kunci type :
Type
Namaarray = array [ 1..5,1..10] of integer ;
var
X : Namaarray :
Contoh-contoh pendeklrasian matrik / array 2 dimensi :
var A : array [ 1..100,1..40] of integer;
var X : array [ 10..15,1..5] of real;
var Z : array [ 1..20,1..5] of char;
Var a : array [ 1..5,1..5] of integer ;
a [ 1 , 5 ] := 5 ; artinya baris ke 1 pada kolom ke 5 akan di isi nilai ( 5 ) ;
a [ 2 , 1 ] := 10 ; artinya baris ke 2 pada kolom ke 1 akan di isi nilai ( 10 ) ;
a [ 3 , 3 ] := 20 ; artinya baris ke 3 pada kolom ke 3 akan di isi nilai ( 20 ) ;
a [ 5 , 5 ] := 15 ; artinya baris ke 5 pada kolom ke 5 akan di isi nilai ( 15 ) ;
Var a : array [ 1..5,1..5] of real ;
a [ 1 , 5 ] := 5,5 ; artinya baris ke 1 pada kolom ke 5 akan di isi nilai ( 5,5 ) ;
a [ 2 , 1 ] := 10,5 ; artinya baris ke 2 pada kolom ke 1 akan di isi nilai ( 10,5 ) ;
Var a : array [ 1..5,1..5] of char ;
a [ 1 , 5 ] := 'A' ; artinya baris ke 1 pada kolom ke 5 akan di isi nilai ( A ) ;
a [ 2 , 1 ] := 'B' ; artinya baris ke 2 pada kolom ke 1 akan di isi nilai ( B ) ;
Contoh Potongan Program Array 2 Dimensi
Pemberian nilai dengan indeks yang bersesuaian dengan perulangan contoh potongan algoritmanya :
Dibawah ini dicontohkan pemberian dengan menggunakan perulangan for do yang masih belum memahami perulangan for do dengan pascal bisa baca link di bawah ini
Baca Juga : Perulangan Pascal Menggunakan Konstruksi FOR - TO - DO Dan DOWNTO
Maka proses 1 :
For I := 1 to 100 do { baris / perulangan luar }
Begin
For J := 1 to 3 do { kolom / perulangan dalam }
begin
Readln(Nilai_mhs[I,J); { [ i , j ] indeks yang bersesuaian }
End;
End;
Maka disini bisa kita sebut perulangan terluar adalah I dan perulangan dalam adalah J dimana perinsip perulangan didalam perulangan adalah bagian perulangan bagian dalam harus di habiskan terlebih dahulu baru kemudian perulangan bagian dalam.
Disini saya mendefinisikan dua buah variabel yaitu I dan J, dimana proses perulangan akan dimulai dari variabel I := 1, Yang kemudian akan berlanjut keperulangan J := 1
disini kode Readln(Nilai_mhs[I,J); Sekarang nilai I dan J mempunyai data didalam [ 1 , 1 ] dan ini mengacu pada indeks array dua dimensi, baris 1 kolom ke 1 dan data yang anda input akan masuk kedalam nya
disini harus di ingat bahwa perulangan lebih dalam harus di habiskan / di eksekusi sampai selesai
Maka proses perulangan dalam 2 :
For I := 1 to 100 do { baris / perulangan luar }
Begin
For J := 2 to 3 do { kolom / perulangan dalam }
begin
Readln(Nilai_mhs[I,J); { [ i , j ] indeks yang bersesuaian }
End;
End;
variabel array Nilai_mhs[ 1, 2 ] ; akan mengacu pada baris ke satu kolom ke dua dan ini mengacu pada indeks array dua dimensi, baris 1 kolom ke 2 dan data yang anda input akan masuk kedalam nya.
Maka proses perulangan dalam 3 :
For I := 1 to 100 do { baris / perulangan luar }
Begin
For J := 3 to 3 do { kolom / perulangan dalam }
begin
Readln(Nilai_mhs[I,J); { [ i , j ] indeks yang bersesuaian }
End;
End;
variabel array Nilai_mhs[ 1, 3 ] ; akan mengacu pada baris ke satu kolom ke dua dan ini mengacu pada indeks array dua dimensi, baris 1 kolom ke 3 dan data yang anda input akan masuk kedalam nya.
Maka Setelah perulangan bagian dalam habis selanjutnya akan di lanjutkan lagi bagian perulangan luar naik satu step menjadi 2 maka jik amelihat contoh kodenya akan menjadi seperti ini
For I := 2 to 100 do { baris / perulangan luar }
Begin
For J := 1 to 3 do { kolom / perulangan dalam }
begin
Readln(Nilai_mhs[I,J); { [ i , j ] indeks yang bersesuaian }
End;
End;
Dst...
Dan perulangan bagian dalam akan dimulai dari start awal lagi dari angka 1. dan begitulah seterusnya proses perulangan berlangsung sampai habis proses perulangan terluar.
variable_array: array ['A'..'C', 'X'..'Z'] of integer;
Misal kita menemui algoritma pembentuk matrik sperti di bawah ini :
Jika melihat gambar 4. terlihat sebuag algoritma dengan menggunakan pseudocode ( sebelah kanan ) untuk membentuk matrik gambar 4 sebelah kiri
Dengan menggunakan nested for dan if else maka matrik akan terbentuk, Disini tidka berpatokan dengan cara seperti diatas saja karena tiap orang mempunyai gaya yang berbeda dalam pembuatan kode atau algoritma diatas.
Proses prinsip sama dengan perulangan di atas hanya disini ada kondis pemilihan if else dimana kondisi if akan memeriksa nilai di dalam variabel i dan j, Contoh diatas di berikan 3 kemungkinan eksekusi
if i = j then A[i,j] ← i * i
Kode diatas jika nila i = j bernilai true maka maka array A[i , j] mempunyai nilai dari hasil i * i, jika salah maka kode berikutnya akan di periksa
else if i > j then A[i,j] ← i + j
kode diatas di eksekusi bila kode sebelumnya bernilai false, dari kode diatas di lakukan pengecekan lagi jika nilai i > j be bernilai true maka array A [i,j] mempunyai nilai dari hasil i + j ; jika nilainya false maka kode terakhir akan di eksekusi
else A[i,j] ← j - i
Kode diatas akan dieksekusi bila kedua kode sebelumnya bernilai false karena kode ini merupakan alternatif terakhir dari sebuah pemilihan.
Contoh penerapan algoritma matrik diatas dengan menggunakan program pascal :
Pada gambar 5 diatas terlihat program dan hasil programnya saat di compile, pada program diatas input data di lakukan dengan mengakses indeksnya langsung seperti yang di contohkan
Tabel[1,1] := 5 ; nilai 5 disimpan dalam array tabel pada indeks ke 1,1
Tabel[1,2] := 25 ; nilai 25 disimpan dalam array tabel pada indeks ke 1,2
Tabel[2,1] := 200 ; nilai 200 disimpan dalam array tabel pada indeks ke 2,1
Tabel[2,2] := 22 ; nilai 22 disimpan dalam array tabel pada indeks ke 2,2
Tabel[3,1] := 75 ; nilai 75 disimpan dalam array tabel pada indeks ke 3,1
Tabel[3,2] := 50 ; nillai 50 disimpan dalam array tabel pada indeks ke 3,2
Setelah nilai tersimpan pada masing masing indeksnya maka untuk mencetak output dapt menggunakan perulangan for seperti tampak pada gambar 5.
ingatlah bahwa perulangan nested for diatas seperti telah di jelaskan di awal konsepnya sam dengan baris dan kolom
Kode baris for i:= 1 to 3 do { Perulangan luar }
Pada output gambar 5 terlihat ada hasilnya, Ada 3 baris kebawah dengan nilai berbeda, Nilai itu adalah nilai yang tersimpan dalam indeks
Kemudian baris for j := 1 to 2 do { Perulangan dalam }
Untuk mencetak baris kesamping seperti output yang terlihat ada 2 kolom dengan nilai berdasarkan nilai yang tersimpan dalam indeks yang ada pada array tabel di kombinasikan dengan perintah write dan writeln agar output dapat kesamping dan turun / mengganti garis baru.
Contoh lain yang mungkin bisa anda praktekan agar anda bisa lebih memahami materi tantang array 2 dimensi adalah program seperti gambar di bawah ini dimana input data dan mencetak output bersasarkan ketersesuaian dengan indeks perulangan
Rumus penjumlahan dan pengurangan menggunakna algoritma vektor
Penjumlahan A + B = C , { A , B , C adalah vektor yang sama )
Pengurangan A - B = C , { A , B , C adalah vektor yang sama )
Definsi :
C(i) = A(i) + B(i) { penjumlahan }
C(i) = A(i) - B(i) { pengurangan }
Algoritmanya Penjumlahan :
for i ← 1 to n do
c[i] ← a[i] + b[i]
endfor
Algoritmanya Pengurangan :
for i ← 1 to n do
c[i] ← a[i] - b[i]
endfor
Bila melihat algoritma diatas pada gambar ( 7 ) maka dilakukan perulangan sampai sejumlah nilai n yang di tentukan dimana nilai a[i] akan di tambah atau dikurangi dengan b[i] tergantung penggunaan operator. kemudian hasilnya akan di tampung didalam variabel c[i]
Penerapan dalam program pascalnya adalah seperti di bawah ini :
Agar lebih paham silahkan anda mencoba program sederhana diatas, untuk program pengurangan silahkan di sesuaikan dengan penggunaan operatornya.
Rumus yang di gunakan adalah A . B = K ; dimana A dan B merupakan Vektor berdimensi sama, K adalah konstanta
Didefinisikan : K = a1 * b1 + a2 * b2 + a3 * b3 + ... + an * bn
Algoritmanya :
k ← 0
for i ← 1 to n do
k ← k + a[i] * b[i]
endfor
Jika melihat dari lagortima diatas tetap perkalian vektor dengan dimensi yang sama diatas k adalah sebuah variabel yang di berikan nilai 0
kemudian dilakukan perulangan for dari 1 sampai nilai n tertentu unutk mendapatkan nilai dari array a[i] dan b[i] yang nilai hasil perkalianya akan di tampung oleh variabel k
Untuk penerapan dalam program pascal bisa lihat di bawah ini :
Silahkan di coba program sederhana diatas untuk memahami lebih dalam tentang algoritmanya.
Pejumlahan matrik dan pengurangan matrik dapat dilakukan bila dua buah matrik A dan B mempunyai domensi sama ( ukuran matrik a sama dengan ukuran matrik b ) dan kedua nilai matrik sudah terdefinisi
Rumus yang di gunakan adalah :
A + B = C { A, B, C adalah matrik yagn berordo sama }
A - B = C { A, B, C adalah matrik yagn berordo sama }
Definisi :
C[i,j] ← A[i,j] + B[i,j] ( penjumlahan ) atau
C[i,j] ← A[i,j] - B[i,j] ( pengurangan )
Algoritmanya :
for i ← 1 to n do
for j ← 1 to n do
c[i,j] ← a[i,j] - b[i,j]
endfor
endfor
Contoh gambar di bawah ini alur proses penjumlahan dan pengurangan matrik
Dicontohkan dengan data :
Penjumlahan matrik A + B dengan data sebagai berikut C[i,j] ← A[i,j] + B[i,j] :
matrik a matrik b matrik c
1 3 5 -6 9 8 -5 12 13
18 31 1 + 3 2 1 = 21 33 2
2 4 15 4 5 -7 6 7 -7
Contoh penerapan dengan menggunakan program pascal untuk penjumlahan dan pengurangan matrik kode di bawah ini menggunakan procedure bab procedure akan di bahas pada artikel lainya :
program MATRIK_penjumlahandapengurangan(2);
uses crt;
type
data = array[1..100,1..100] of integer;
var
matrikI,matrikII : data;
baris,kolom, pil:integer;
procedure isimatrik;
var i,j : integer;
begin
writeln('MATRIK A');
write('Masukan Jumlah Baris = ');readln(baris);
write('Masukan Jumlah Kolom = ');readln(kolom);
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
readln(matrikI[i,j]);
end;
clrscr;
writeln('MATRIK B');
write('Masukan Jumlah Baris = ');readln(baris);
write('Masukan Jumlah Kolom = ');readln(kolom);
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
readln(matrikII[i,j]);
end;
end;
procedure jumlahmatrik(m1,m2 : data);
var hasil : data;
i,j : integer;
begin
for i:=1 to baris do
for j:=1 to kolom do
begin
hasil[i,j]:= m1[i,j] + m2[i,j];
end;
clrscr;
writeln('Hasil Penjumlahan MATRIK');
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
write(hasil[i,j]);
end;
readln;
end;
procedure kurangmatrik(m1,m2 : data);
var hasil : data;
i,j : integer;
begin
for i:=1 to baris do
for j:=1 to kolom do
begin
hasil[i,j]:=m1[i,j]-m2[i,j];
end;
clrscr;
writeln('Hasil Pengurangan MATRIK');
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
write(hasil[i,j]);
end;
readln;
end;
BEGIN
repeat
Clrscr;
writeln;
writeln;
writeln('Menu Pilihan ');
writeln;
writeln('Input ( 1 ) Penjumlahan Matrik');
writeln('Input ( 2 ) Pengurangan Matrik');
writeln('input ( 3 ) Exit Program');
writeln;
write('Pilihan = ');readln(pil);
clrscr;
case pil of
1 : begin
writeln(' Penjumlahan Matrik ');
isimatrik;
jumlahmatrik(matrikI,matrikII);
end;
2 : begin
writeln(' Kurang Matrik ');
isimatrik;
kurangmatrik(matrikI,matrikII);
end;
3 : ;
end;
until pil=3;
end.
Hasil dari compilasi program matrik menggunakan bahasa pascal diatas adalah sebagai berikut :
Gambar 13 adalah hasil kompilasi program pascal sederhana mungkin setiap orang akan berbeda source code / kode program tetapi intinya sama bagaimana menggunakan rumus operasi matrik dan menerapkan kedalam pemrograman pascal sehingga secara teori dan hasil tetap sama.
4. Operasi Perkalian matrik dengan matrik dengan ketentuan yaitu perkalian matrik A dengan matrik B adalah perkalian, Baris matrik A dengan Kolom matrik B.
A X B = C { C merupakan matrik berordo N * N )
Contoh :
A . B = | a b | * | k l | = | ak + bm al + bn |
| c d | | m n | | ck + dm cl + dn |
Perhatikan gambar di bawah ini capek nulisnya ( :V ) :
Duh matrik kali matrik rade susah ne jelasinye di katakan dengan indah sebelumnya ente harus paham dulu array dua dimensi ye konsep baris dan kolom kalo you belum paham yee scrool keatas lagi baca lagi ampe seratus kali biar paham.... udah paham baru lanjut lagi kesini yee
Begini sodare kjesafiua;b;kua vsa'hvoSj'bvsbv'sbkjvvsbvdkjusbjsbc'sasvw
awhgiaowvkjsavkabsiuasbdviusabvdiuwav sjdskjdskjbdsdsfskdkjsbkjsbdf akfbakjb asashsafbvugAFABKJASBKJABAKJkjzbfdkjsbdvsdskjbvskjb
Svdiuawvsab;hsbaivsvwaga.... udah paham blm, udah di jelasin panjang lebar juga (:V) masih blm paham. lagi duh ( :V :V :V )
Ya udeh you liat contoh programnya di bawah ini dulu ye terus, di praktekin tulis tuh di IDE nya pascal ( free pascal ) atau bisa pake yang lain jangan di copas yee percuma dosa tar you, udeh gak paham di copas lagi. di ketik satu persatu biar nempel di OTAK bader banget sih dibilanginye.
for i:=1 to baris do { perulangan untuk baris }
for j:=1 to kolom do { perulangan untuk kolom }
begin
hasil[i,j]:=0; { kasih dulu nilai 0 ye }
for z:=1 to baris do
{ ini perulangan juga ye gak usah pusing fungsinya, liat angkanya ajah, dia melakukan perulangan dari 1 sampai nilai baris, kalo nilai baris 1 ya dia muter 1 kali, kalo baris nilaianya 2 dia muter 2 kali }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
{ Nah disni nih yang penting hasil[i,j] ini awalnya kan 0 terus akan bertambah nilaianya sampai perulangan for yang ketiga yaitu Z habis
Misal data aray beordo 2 X 2 maka disini di ambil kesimpulan ada 3 looping, dimana tiap looping berputar 2 kali, loop paling luar yang diinisialisasi ( i ) kita sebut loop baris ini akan dua kali loop
Loop kedua yang diinisialisasi oleh ( j ) ini kita sebut loop kedua ( kolom ).
Loop ketiga yang di inisialisasi oleh Z ini loop ketiga disini kita melihat angkanya saja untuk mengakses indeks pada array matrik, baik itu matrikA atau matrikB.
Misalnya kita membayangkan sebuah array dengan visual tabel dengan no indeks akan seperti tabel berikut. dan data elemen yg sudah kalian input dan tersimpan dalam memori adalah sebagai berikut
Tabel memori matrik berordo 2 X 2 :
indeks matrik A matrik B
1,1 | 2 | | 1 |
1,2 | 3 | | 3 |
2,1 | 5 | | 4 |
2,2 | 2 | | 2 |
Misal bila data di proses oleh perogram adalah sebagai berikut ingat perulangan paling dalam akan di eksekusi terlebih dahulu sampai selesai baru kemudian perulangan luar. Dan ini dimulai langsung dari loop ketiga lalu loop kedua dan loop pertama secara berurutan.
for i:=1 to baris do { i disini 1 }
for j:=1 to kolom do { j disini 1 }
begin
for z:=1 to baris do { z disini 1 }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
Loop ketiga Z tahap pertama :
Matrik A[1,1] lihat tabel matrik A 1,1 elemenya bernilai ( 2 ), MatrkiB [1,1] lihat juga tabel matrik B elemenya ( 1 ), nilai matrikA(2) * matrikB(1) = 2
hasil [i,j] bernilai 0 nah ini akan di tambahkan dengan nilai 2 ( 0 + 2 = 2 ). hasil perkalian matrik A dan B pada lopp z (pertama ). dan nilainya disimpan sementara di hasil[i,j] tersimpan nilai 2.
loop Z tahap kedua :
for i:=1 to baris do { i disini 1 }
for j:=1 to kolom do { j disini 1 }
begin
for z:=1 to baris do { z disini 2 }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
Matrik A[1,2] lihat tabel matrikA 1,2 elemenya bernilai ( 3 ), MatrikB [2,1] lihat juga tabel matrik B elemenya ( 4 ), nilai matrikA(3) * matrikB(4) = 12
Maka nilai yang tersimpan sementara tadi 2 + 12 = 14 ( tersimpan sementara di memori )
Dan karena ini loop terakhir maka hasil[i,j] atau jika berdasarkan akses indeks maka hasil[1,1] = 14
Loop ketiga ( z ) berakhir maka loop kedua ( j ) naik satu tingkat lagi bernilai 2 dan loop ketiga dimulai lagi dari angka 1 :
for i:=1 to baris do { i disini 1 }
for j:=1 to kolom do { j disini 2 }
begin
for z:=1 to baris do { z disini 1 }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
Matrik A[1,1] lihat tabel matrik A 1,1 elemenya bernilai ( 2 ), MatrkiB [1,2] lihat juga tabel matrik B elemenya ( 3 ), nilai matrikA(2) * matrikB(3) = 6
hasil [i,j] bernilai 0 nah ini akan di tambahkan dengan nilai 6 ( 0 + 6 = 6 ). hasil perkalian matrik A dan B pada lopp z (pertama ). dan nilainya disimpan sementara di hasil[i,j] tersimpan nilai 6.
loop Z tahap kedua :
for i:=1 to baris do { i disini 1 }
for j:=1 to kolom do { j disini 2 }
begin
for z:=1 to baris do { z disini 2 }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
Matrik A[1,2] lihat tabel matrikA 1,2 elemenya bernilai ( 3 ), MatrikB [2,2] lihat juga tabel matrik B elemenya ( 2 ), nilai matrikA(3) * matrikB(2) = 6
Maka nilai yang tersimpan sementara tadi 6 + 6 = 12 ( tersimpan sementara di memori )
Dan karena ini loop terakhir maka hasil[i,j] atau jika berdasarkan akses indeks maka hasil[1,2] = 12
Dan ketika loop kedua habis di eksekusi loop paling luar akan naik tingkat lagi yang tadinya i bernilai ( 1 ) akan bernilai ( 2 ) itu artinya loop akan berpindah baris.
Dan proses akan terulang seperti awal lagi terus menerus sampai hasilnya akan seperti gambar di bawah ini jika program di runing :
Lebih mudah memahami program sebenarnya jika di banding harus memahami algoritmanya, Penjelasan diatas kalo di jabarkan akan sangat panjang ( :V ) dan capek ngetiknya. lagian biasanya gak dibaca juga karena rumit mungkin ( :V ) mending compile codenya dan di pahami akan lebih mudah.
Perkalian matrik dengan vektor adalah perkalian N * N, simpelnya jika matrik A x B maka jumlah kolom matrik B harus sama dengan jumlah baris matrik A .
Agar lebih hemat waktu silahkan lihat gambar 16 di bawah ini :
Kali ini tidak di jabarkan karena dengan melihat gambarnya saja tentunya kalian sudah paham apa lagi setelah membaca perkalian matrik * matrik tentunya proses didalam program sama saja dan ini lebih mudah syaratnya hanya
Jumlah kolom matrik B harus sama dengn jumlah baris matrik A .
Agar lebih memahami silahkan lihat source code di bawah ini agar lebih paham dan jelas :
Hasil program diatas adalah siperti tampak gambar di bawah ini :
Baca Juga : Algoritma 2 : Pengertian Procedure Dan Penerapan Dalam Bahasa Pascal
Nah pembahasan kita tentang array matrik dan operasi perkalian, penjumlahan , pengurangan matrik serta perkalian matrik x vektor sampai disini pembahasanya tetaplah belajar sampai ilmu itu bisa berbicara dengan anda karena ilmu itu memilih tempat, bukan anda yang memilihnya luruskan niat anda dengan benar untuk mencari ilmu - ilmuit.id
 |
| Algoritma 2 : Array Dua Dimensi Beserta Contoh Program Pascal |
Baca Juga : Tutorial Pemrograman Pascal Dasar
Dimana pengertian array dua dimensi menurut para pakar adalah sebagai berikut :
Raharjo ( 2010:140 ) "array dua dimensi adalah array yang memiliki dua buah elemen bertipe array, dengan kata lain array dua dimensi mempunyai subskrip yang biasanya di presentasikan dengan baris dan kolom"
Ramadhani ( 2015: 59 ) "array dimensi dua sering di analogikan sebagai sebuah matrik jika array dimensi satu hanya terdiri atas satu baris dan banyak kolom, array diemnsi dua terdiri dari banyak baris dan banyak kolom yang bertipe sama"
Baca Juga : Algoritma 2 : Pembahasan Tentang Larik / Array 1 dimensi
Perbedaan antara array 1 dimensi dan array 2 dimensi
Array 1 dimensi terdiri dari satu baris dan banyak kolom, Sedangkan array 2 dimensi terdiri dari banyak baris dan banyak kolom jika di presentasikan secara visual maka kita dapat melihat array dua dimensi seperti di bawah ini
Misalkan di contohkan secara visual :
 |
| Gambar 1 : array2 dimensi ( baris X kolom = 3 X 4 ) |
Maka jika ada baris kode matrik / array dua dimensi seperti ini menggunakan bahasa pasca
var data : array [ 1..50, 1..100 ] of integer ;
Maka berarti anda telah menyiapkan 50 baris dan 100 kolom di memori. indeks pertama di tunjukan oleh angka 1..50 dan indeks kedua di tunjukan oleh angka 1..100.
Tanda ( , ) pada [ 1..50 , 1..100 ] untuk memisahkan indeks pertama dan indeks kedua.
Contoh lainya :
var
Nilai_mhs : array [1..100,1..3] of Integer;
Maka jika di repsentasikan secara visual dengan gambar akan seperti di bawah ini
![array [1..10,1..3] array [1..10,1..3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgrXIppzZ5POgPezZD0ZO8zmic2JB-aO1fm_TuQ19P-hmD0oAyeefWauuf4a6dBlJ1R35Zs3Lp-6QZJ863lPTLG-Oe7UNIfnXZnLpAn7UpfqakHSHOptVoRzJxRCzmWU-W19B3_UKFPvkTt/s640/ar8.jpg) |
| Gambar 2 : array [ 1..100,1..3] of integer |
Cara Mendeklarasikan Array 2 Dimensi / Matrik
Unutk mendeklarasikan array 2 dimensi pada pemrograman pascal anda bisa menempatkan kodenya pada bagian TYPE atau VARVar namaarray : array [ 1..5,1..10] of integer ;
Menggunakan kata kunci type :
Type
Namaarray = array [ 1..5,1..10] of integer ;
var
X : Namaarray :
Contoh-contoh pendeklrasian matrik / array 2 dimensi :
var A : array [ 1..100,1..40] of integer;
var X : array [ 10..15,1..5] of real;
var Z : array [ 1..20,1..5] of char;
Pemberian Nilai Untuk Satu Elemen Matrik
Untuk memasukan data pada array dimensi 2 harus menyebutkan no indeks baris dan no indeks kolom, Dibawah ini adalah contoh cara untuk memasukan nilai kedalam elemen matrik dengan pascal :Var a : array [ 1..5,1..5] of integer ;
a [ 1 , 5 ] := 5 ; artinya baris ke 1 pada kolom ke 5 akan di isi nilai ( 5 ) ;
a [ 2 , 1 ] := 10 ; artinya baris ke 2 pada kolom ke 1 akan di isi nilai ( 10 ) ;
a [ 3 , 3 ] := 20 ; artinya baris ke 3 pada kolom ke 3 akan di isi nilai ( 20 ) ;
a [ 5 , 5 ] := 15 ; artinya baris ke 5 pada kolom ke 5 akan di isi nilai ( 15 ) ;
Var a : array [ 1..5,1..5] of real ;
a [ 1 , 5 ] := 5,5 ; artinya baris ke 1 pada kolom ke 5 akan di isi nilai ( 5,5 ) ;
a [ 2 , 1 ] := 10,5 ; artinya baris ke 2 pada kolom ke 1 akan di isi nilai ( 10,5 ) ;
Var a : array [ 1..5,1..5] of char ;
a [ 1 , 5 ] := 'A' ; artinya baris ke 1 pada kolom ke 5 akan di isi nilai ( A ) ;
a [ 2 , 1 ] := 'B' ; artinya baris ke 2 pada kolom ke 1 akan di isi nilai ( B ) ;
Contoh Potongan Program Array 2 Dimensi
 |
| Gambar 3 :Pemberian nilai array matrik dengan pascal |
Dibawah ini dicontohkan pemberian dengan menggunakan perulangan for do yang masih belum memahami perulangan for do dengan pascal bisa baca link di bawah ini
Baca Juga : Perulangan Pascal Menggunakan Konstruksi FOR - TO - DO Dan DOWNTO
Maka proses 1 :
For I := 1 to 100 do { baris / perulangan luar }
Begin
For J := 1 to 3 do { kolom / perulangan dalam }
begin
Readln(Nilai_mhs[I,J); { [ i , j ] indeks yang bersesuaian }
End;
End;
Maka disini bisa kita sebut perulangan terluar adalah I dan perulangan dalam adalah J dimana perinsip perulangan didalam perulangan adalah bagian perulangan bagian dalam harus di habiskan terlebih dahulu baru kemudian perulangan bagian dalam.
Disini saya mendefinisikan dua buah variabel yaitu I dan J, dimana proses perulangan akan dimulai dari variabel I := 1, Yang kemudian akan berlanjut keperulangan J := 1
disini kode Readln(Nilai_mhs[I,J); Sekarang nilai I dan J mempunyai data didalam [ 1 , 1 ] dan ini mengacu pada indeks array dua dimensi, baris 1 kolom ke 1 dan data yang anda input akan masuk kedalam nya
disini harus di ingat bahwa perulangan lebih dalam harus di habiskan / di eksekusi sampai selesai
Maka proses perulangan dalam 2 :
For I := 1 to 100 do { baris / perulangan luar }
Begin
For J := 2 to 3 do { kolom / perulangan dalam }
begin
Readln(Nilai_mhs[I,J); { [ i , j ] indeks yang bersesuaian }
End;
End;
variabel array Nilai_mhs[ 1, 2 ] ; akan mengacu pada baris ke satu kolom ke dua dan ini mengacu pada indeks array dua dimensi, baris 1 kolom ke 2 dan data yang anda input akan masuk kedalam nya.
Maka proses perulangan dalam 3 :
For I := 1 to 100 do { baris / perulangan luar }
Begin
For J := 3 to 3 do { kolom / perulangan dalam }
begin
Readln(Nilai_mhs[I,J); { [ i , j ] indeks yang bersesuaian }
End;
End;
variabel array Nilai_mhs[ 1, 3 ] ; akan mengacu pada baris ke satu kolom ke dua dan ini mengacu pada indeks array dua dimensi, baris 1 kolom ke 3 dan data yang anda input akan masuk kedalam nya.
Maka Setelah perulangan bagian dalam habis selanjutnya akan di lanjutkan lagi bagian perulangan luar naik satu step menjadi 2 maka jik amelihat contoh kodenya akan menjadi seperti ini
For I := 2 to 100 do { baris / perulangan luar }
Begin
For J := 1 to 3 do { kolom / perulangan dalam }
begin
Readln(Nilai_mhs[I,J); { [ i , j ] indeks yang bersesuaian }
End;
End;
Dst...
Dan perulangan bagian dalam akan dimulai dari start awal lagi dari angka 1. dan begitulah seterusnya proses perulangan berlangsung sampai habis proses perulangan terluar.
Contoh Array 2 Dimensi Menggunakan Indeks Karakter
Pada array 2 dimensi kita juga dapat menggunakan indeks dengan menggunakan karakter seperti contoh di bawah ini di buat menggunakan bahasa pascal.
Cara deklarasi adalah :
untuk lebih jelasnya teman teman bisa lihat gambar di bawah ini :
Dari gamabr di atas di contohkan penggunaan array 2 dimensi menggunakan indeks karakter sangat mudah bukan. dan output yang di hasikan adalah di bawah ini :
Contoh Algoritma Membentuk Matrik
Misal kita menemui algoritma pembentuk matrik sperti di bawah ini : |
| Gambar 4 : algortima penyusun matrik |
Dengan menggunakan nested for dan if else maka matrik akan terbentuk, Disini tidka berpatokan dengan cara seperti diatas saja karena tiap orang mempunyai gaya yang berbeda dalam pembuatan kode atau algoritma diatas.
Proses prinsip sama dengan perulangan di atas hanya disini ada kondis pemilihan if else dimana kondisi if akan memeriksa nilai di dalam variabel i dan j, Contoh diatas di berikan 3 kemungkinan eksekusi
if i = j then A[i,j] ← i * i
Kode diatas jika nila i = j bernilai true maka maka array A[i , j] mempunyai nilai dari hasil i * i, jika salah maka kode berikutnya akan di periksa
else if i > j then A[i,j] ← i + j
kode diatas di eksekusi bila kode sebelumnya bernilai false, dari kode diatas di lakukan pengecekan lagi jika nilai i > j be bernilai true maka array A [i,j] mempunyai nilai dari hasil i + j ; jika nilainya false maka kode terakhir akan di eksekusi
else A[i,j] ← j - i
Kode diatas akan dieksekusi bila kedua kode sebelumnya bernilai false karena kode ini merupakan alternatif terakhir dari sebuah pemilihan.
Contoh penerapan algoritma matrik diatas dengan menggunakan program pascal :
 |
| Gambar 5 : program matrik sederhana menggunakan pascal |
Tabel[1,1] := 5 ; nilai 5 disimpan dalam array tabel pada indeks ke 1,1
Tabel[1,2] := 25 ; nilai 25 disimpan dalam array tabel pada indeks ke 1,2
Tabel[2,1] := 200 ; nilai 200 disimpan dalam array tabel pada indeks ke 2,1
Tabel[2,2] := 22 ; nilai 22 disimpan dalam array tabel pada indeks ke 2,2
Tabel[3,1] := 75 ; nilai 75 disimpan dalam array tabel pada indeks ke 3,1
Tabel[3,2] := 50 ; nillai 50 disimpan dalam array tabel pada indeks ke 3,2
Setelah nilai tersimpan pada masing masing indeksnya maka untuk mencetak output dapt menggunakan perulangan for seperti tampak pada gambar 5.
ingatlah bahwa perulangan nested for diatas seperti telah di jelaskan di awal konsepnya sam dengan baris dan kolom
Kode baris for i:= 1 to 3 do { Perulangan luar }
Pada output gambar 5 terlihat ada hasilnya, Ada 3 baris kebawah dengan nilai berbeda, Nilai itu adalah nilai yang tersimpan dalam indeks
Kemudian baris for j := 1 to 2 do { Perulangan dalam }
Untuk mencetak baris kesamping seperti output yang terlihat ada 2 kolom dengan nilai berdasarkan nilai yang tersimpan dalam indeks yang ada pada array tabel di kombinasikan dengan perintah write dan writeln agar output dapat kesamping dan turun / mengganti garis baru.
Contoh lain yang mungkin bisa anda praktekan agar anda bisa lebih memahami materi tantang array 2 dimensi adalah program seperti gambar di bawah ini dimana input data dan mencetak output bersasarkan ketersesuaian dengan indeks perulangan
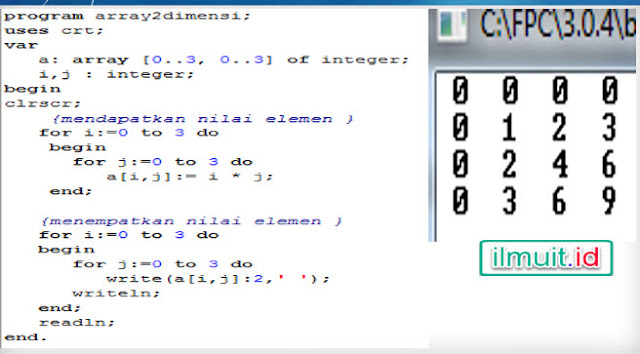 | |
| Gambar 6 : matrik dengan perulangan for |
Algoritma-algoritma Operasi Vektor dan Matriks
Disini hal yang kita bahas tidak mendalam mengenai rumus. disini kita hanya memfocuskan mengetahui rumus-rumus tersebut, Karena pembahasan mengenai rumus masih banyak pakar yang lebih competen untuk membahasanya.
1. Penjumlahan Dan Pengurangan Operasi Vektor ( 1 Dimensi )
Rumus penjumlahan dan pengurangan menggunakna algoritma vektor
Penjumlahan A + B = C , { A , B , C adalah vektor yang sama )
Pengurangan A - B = C , { A , B , C adalah vektor yang sama )
Definsi :
C(i) = A(i) + B(i) { penjumlahan }
C(i) = A(i) - B(i) { pengurangan }
Algoritmanya Penjumlahan :
for i ← 1 to n do
c[i] ← a[i] + b[i]
endfor
Algoritmanya Pengurangan :
for i ← 1 to n do
c[i] ← a[i] - b[i]
endfor
 |
| Gambar 7 : algoritma vektor penjumlahan dan pengurangan |
Bila melihat algoritma diatas pada gambar ( 7 ) maka dilakukan perulangan sampai sejumlah nilai n yang di tentukan dimana nilai a[i] akan di tambah atau dikurangi dengan b[i] tergantung penggunaan operator. kemudian hasilnya akan di tampung didalam variabel c[i]
Penerapan dalam program pascalnya adalah seperti di bawah ini :
program vektor1;
uses crt;
type
data = array[1..100] of integer ;
var
a,b,c : data;
i,n : integer;
begin
clrscr;
writeln('program array');
writeln('=============');
writeln;
write ('masukan jumlah data : '); readln(n);
writeln();
for i:= 1 to n do
begin
write ('input data array ',i,' ke : '); readln(a[i]);
end;
writeln;
for i:= 1 to n do
begin
write ('input data array',i,' ke : '); readln(b[i]);
end;
for i:= 1 to n do
begin
c[i]:= a[i] + b[i];
end;
writeln;
writeln('hasil penjumlahan:');
writeln;
for i := 1 to n do
writeln(' ',c[i],' ');
readln;
end.
uses crt;
type
data = array[1..100] of integer ;
var
a,b,c : data;
i,n : integer;
begin
clrscr;
writeln('program array');
writeln('=============');
writeln;
write ('masukan jumlah data : '); readln(n);
writeln();
for i:= 1 to n do
begin
write ('input data array ',i,' ke : '); readln(a[i]);
end;
writeln;
for i:= 1 to n do
begin
write ('input data array',i,' ke : '); readln(b[i]);
end;
for i:= 1 to n do
begin
c[i]:= a[i] + b[i];
end;
writeln;
writeln('hasil penjumlahan:');
writeln;
for i := 1 to n do
writeln(' ',c[i],' ');
readln;
end.
Agar lebih paham silahkan anda mencoba program sederhana diatas, untuk program pengurangan silahkan di sesuaikan dengan penggunaan operatornya.
 |
| gambar 8 : Program Penjumlahan Dan Pengurangan Operasi Vektor ( 1 Dimensi ) |
2. Operasi Perkalian Vektor ( 1 Dimensi )
Rumus yang di gunakan adalah A . B = K ; dimana A dan B merupakan Vektor berdimensi sama, K adalah konstanta
Didefinisikan : K = a1 * b1 + a2 * b2 + a3 * b3 + ... + an * bn
Algoritmanya :
k ← 0
for i ← 1 to n do
k ← k + a[i] * b[i]
endfor
 |
| gamabar 9 : algoritma Operasi Perkalian Vektor ( 1 Dimensi ) |
Jika melihat dari lagortima diatas tetap perkalian vektor dengan dimensi yang sama diatas k adalah sebuah variabel yang di berikan nilai 0
kemudian dilakukan perulangan for dari 1 sampai nilai n tertentu unutk mendapatkan nilai dari array a[i] dan b[i] yang nilai hasil perkalianya akan di tampung oleh variabel k
Untuk penerapan dalam program pascal bisa lihat di bawah ini :
program array1vektor_Perkalian;
uses crt;
type
Vektor = array [1..100] of integer;
var
a,b,c : Vektor;
n, i ,k : integer;
begin
clrscr;
writeln ('program array vektor perkalian');
writeln ('======================');
writeln;
write (' masukan jumlah data : ');readln(n);
writeln;
for i:= 1 to n do begin
write ('input data array a ke : ');
readln(a[i]);
end;
writeln;
writeln;
for i:= 1 to n do begin
write ('input data array b ke : ');
readln(b[i]);
end;
k:=0;
for i:= 1 to n do begin
k:= k + a[i] * b[i];
end;
writeln;
writeln('hasil.dot product:');
writeln;
{for i := 1 to n do }
writeln(' ',k,' ');
readln;
end.
uses crt;
type
Vektor = array [1..100] of integer;
var
a,b,c : Vektor;
n, i ,k : integer;
begin
clrscr;
writeln ('program array vektor perkalian');
writeln ('======================');
writeln;
write (' masukan jumlah data : ');readln(n);
writeln;
for i:= 1 to n do begin
write ('input data array a ke : ');
readln(a[i]);
end;
writeln;
writeln;
for i:= 1 to n do begin
write ('input data array b ke : ');
readln(b[i]);
end;
k:=0;
for i:= 1 to n do begin
k:= k + a[i] * b[i];
end;
writeln;
writeln('hasil.dot product:');
writeln;
{for i := 1 to n do }
writeln(' ',k,' ');
readln;
end.
Silahkan di coba program sederhana diatas untuk memahami lebih dalam tentang algoritmanya.
 |
| gambar 10 : Hasil Penerapan Program pascal Operasi Perkalian Vektor ( 1 Dimensi ) |
3. Operasi Penjumlahan dan Pengurangan Matrik ( array 2 dimensi )
Pejumlahan matrik dan pengurangan matrik dapat dilakukan bila dua buah matrik A dan B mempunyai domensi sama ( ukuran matrik a sama dengan ukuran matrik b ) dan kedua nilai matrik sudah terdefinisi
Rumus yang di gunakan adalah :
A + B = C { A, B, C adalah matrik yagn berordo sama }
A - B = C { A, B, C adalah matrik yagn berordo sama }
Definisi :
C[i,j] ← A[i,j] + B[i,j] ( penjumlahan ) atau
C[i,j] ← A[i,j] - B[i,j] ( pengurangan )
Algoritmanya :
for i ← 1 to n do
for j ← 1 to n do
c[i,j] ← a[i,j] - b[i,j]
endfor
endfor
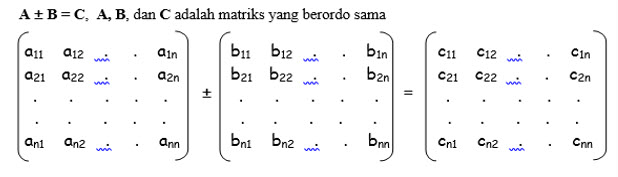 |
| Gambar 11 :Operasi Penjumlahan dan Pengurangan Matrik ( array 2 dimensi ) |
Contoh gambar di bawah ini alur proses penjumlahan dan pengurangan matrik
 |
| gambar 12 :alur proses penjumlahan / pengurangan matrik |
Penjumlahan matrik A + B dengan data sebagai berikut C[i,j] ← A[i,j] + B[i,j] :
matrik a matrik b matrik c
1 3 5 -6 9 8 -5 12 13
18 31 1 + 3 2 1 = 21 33 2
2 4 15 4 5 -7 6 7 -7
Contoh penerapan dengan menggunakan program pascal untuk penjumlahan dan pengurangan matrik kode di bawah ini menggunakan procedure bab procedure akan di bahas pada artikel lainya :
program MATRIK_penjumlahandapengurangan(2);
uses crt;
type
data = array[1..100,1..100] of integer;
var
matrikI,matrikII : data;
baris,kolom, pil:integer;
procedure isimatrik;
var i,j : integer;
begin
writeln('MATRIK A');
write('Masukan Jumlah Baris = ');readln(baris);
write('Masukan Jumlah Kolom = ');readln(kolom);
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
readln(matrikI[i,j]);
end;
clrscr;
writeln('MATRIK B');
write('Masukan Jumlah Baris = ');readln(baris);
write('Masukan Jumlah Kolom = ');readln(kolom);
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
readln(matrikII[i,j]);
end;
end;
procedure jumlahmatrik(m1,m2 : data);
var hasil : data;
i,j : integer;
begin
for i:=1 to baris do
for j:=1 to kolom do
begin
hasil[i,j]:= m1[i,j] + m2[i,j];
end;
clrscr;
writeln('Hasil Penjumlahan MATRIK');
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
write(hasil[i,j]);
end;
readln;
end;
procedure kurangmatrik(m1,m2 : data);
var hasil : data;
i,j : integer;
begin
for i:=1 to baris do
for j:=1 to kolom do
begin
hasil[i,j]:=m1[i,j]-m2[i,j];
end;
clrscr;
writeln('Hasil Pengurangan MATRIK');
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
write(hasil[i,j]);
end;
readln;
end;
BEGIN
repeat
Clrscr;
writeln;
writeln;
writeln('Menu Pilihan ');
writeln;
writeln('Input ( 1 ) Penjumlahan Matrik');
writeln('Input ( 2 ) Pengurangan Matrik');
writeln('input ( 3 ) Exit Program');
writeln;
write('Pilihan = ');readln(pil);
clrscr;
case pil of
1 : begin
writeln(' Penjumlahan Matrik ');
isimatrik;
jumlahmatrik(matrikI,matrikII);
end;
2 : begin
writeln(' Kurang Matrik ');
isimatrik;
kurangmatrik(matrikI,matrikII);
end;
3 : ;
end;
until pil=3;
end.
Hasil dari compilasi program matrik menggunakan bahasa pascal diatas adalah sebagai berikut :
 |
| gamabar 13 : hasil kompilasi program pascal matrik penjumlahand dan pengurangan |
4. Operasi Perkalian matrik dengan matrik dengan ketentuan yaitu perkalian matrik A dengan matrik B adalah perkalian, Baris matrik A dengan Kolom matrik B.
A X B = C { C merupakan matrik berordo N * N )
Contoh :
A . B = | a b | * | k l | = | ak + bm al + bn |
| c d | | m n | | ck + dm cl + dn |
Perhatikan gambar di bawah ini capek nulisnya ( :V ) :
 |
| gambar 14 : Contoh perkalian matrik dengan matrik |
Duh matrik kali matrik rade susah ne jelasinye di katakan dengan indah sebelumnya ente harus paham dulu array dua dimensi ye konsep baris dan kolom kalo you belum paham yee scrool keatas lagi baca lagi ampe seratus kali biar paham.... udah paham baru lanjut lagi kesini yee
Begini sodare kjesafiua;b;kua vsa'hvoSj'bvsbv'sbkjvvsbvdkjusbjsbc'sasvw
awhgiaowvkjsavkabsiuasbdviusabvdiuwav sjdskjdskjbdsdsfskdkjsbkjsbdf akfbakjb asashsafbvugAFABKJASBKJABAKJkjzbfdkjsbdvsdskjbvskjb
Svdiuawvsab;hsbaivsvwaga.... udah paham blm, udah di jelasin panjang lebar juga (:V) masih blm paham. lagi duh ( :V :V :V )
Ya udeh you liat contoh programnya di bawah ini dulu ye terus, di praktekin tulis tuh di IDE nya pascal ( free pascal ) atau bisa pake yang lain jangan di copas yee percuma dosa tar you, udeh gak paham di copas lagi. di ketik satu persatu biar nempel di OTAK bader banget sih dibilanginye.
program MATRIKkalimatrik_3;
uses crt;
type
data = array[1..100,1..100] of integer;
var
matrikA,matrikB : data;
baris,kolom, pil:integer;
procedure isimatrik;
var i,j : integer;
begin
clrscr;
writeln('MATRIK A');
write('Masukan Jumlah Baris = ');readln(baris);
write('Masukan Jumlah Kolom = ');readln(kolom);
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
readln(matrikA[i,j]);
end;
clrscr;
writeln('MATRIK B');
write('Masukan Jumlah Baris = ');readln(baris);
write('Masukan Jumlah Kolom = ');readln(kolom);
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
readln(matrikB[i,j]);
end;
end;
procedure kalimatrik(m1,m2 : data);
var hasil : data;
i,j,z : integer;
begin
for i:=1 to baris do
for j:=1 to kolom do
begin
hasil[i,j]:=0;
for z:=1 to baris do
hasil[i,j]:=hasil[i,j]+matrikA[i,z] * matrikB[z,j];
end;
clrscr;
writeln('Hasil Perkalian MATRIK');
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
write(hasil[i,j]);
end;
readln;
end;
BEGIN
clrscr;
writeln;
writeln;
writeln('Matrik X Matrik ');
writeln;
isimatrik;
kalimatrik(matrikA,matrikB);
readln ;
end.
uses crt;
type
data = array[1..100,1..100] of integer;
var
matrikA,matrikB : data;
baris,kolom, pil:integer;
procedure isimatrik;
var i,j : integer;
begin
clrscr;
writeln('MATRIK A');
write('Masukan Jumlah Baris = ');readln(baris);
write('Masukan Jumlah Kolom = ');readln(kolom);
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
readln(matrikA[i,j]);
end;
clrscr;
writeln('MATRIK B');
write('Masukan Jumlah Baris = ');readln(baris);
write('Masukan Jumlah Kolom = ');readln(kolom);
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
readln(matrikB[i,j]);
end;
end;
procedure kalimatrik(m1,m2 : data);
var hasil : data;
i,j,z : integer;
begin
for i:=1 to baris do
for j:=1 to kolom do
begin
hasil[i,j]:=0;
for z:=1 to baris do
hasil[i,j]:=hasil[i,j]+matrikA[i,z] * matrikB[z,j];
end;
clrscr;
writeln('Hasil Perkalian MATRIK');
for i:=1 to baris do
for j:=1 to kolom do
begin
gotoxy(j*10,i*5);
write(hasil[i,j]);
end;
readln;
end;
BEGIN
clrscr;
writeln;
writeln;
writeln('Matrik X Matrik ');
writeln;
isimatrik;
kalimatrik(matrikA,matrikB);
readln ;
end.
for i:=1 to baris do { perulangan untuk baris }
for j:=1 to kolom do { perulangan untuk kolom }
begin
hasil[i,j]:=0; { kasih dulu nilai 0 ye }
for z:=1 to baris do
{ ini perulangan juga ye gak usah pusing fungsinya, liat angkanya ajah, dia melakukan perulangan dari 1 sampai nilai baris, kalo nilai baris 1 ya dia muter 1 kali, kalo baris nilaianya 2 dia muter 2 kali }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
{ Nah disni nih yang penting hasil[i,j] ini awalnya kan 0 terus akan bertambah nilaianya sampai perulangan for yang ketiga yaitu Z habis
Misal data aray beordo 2 X 2 maka disini di ambil kesimpulan ada 3 looping, dimana tiap looping berputar 2 kali, loop paling luar yang diinisialisasi ( i ) kita sebut loop baris ini akan dua kali loop
Loop kedua yang diinisialisasi oleh ( j ) ini kita sebut loop kedua ( kolom ).
Loop ketiga yang di inisialisasi oleh Z ini loop ketiga disini kita melihat angkanya saja untuk mengakses indeks pada array matrik, baik itu matrikA atau matrikB.
Misalnya kita membayangkan sebuah array dengan visual tabel dengan no indeks akan seperti tabel berikut. dan data elemen yg sudah kalian input dan tersimpan dalam memori adalah sebagai berikut
Tabel memori matrik berordo 2 X 2 :
indeks matrik A matrik B
1,1 | 2 | | 1 |
1,2 | 3 | | 3 |
2,1 | 5 | | 4 |
2,2 | 2 | | 2 |
Misal bila data di proses oleh perogram adalah sebagai berikut ingat perulangan paling dalam akan di eksekusi terlebih dahulu sampai selesai baru kemudian perulangan luar. Dan ini dimulai langsung dari loop ketiga lalu loop kedua dan loop pertama secara berurutan.
for i:=1 to baris do { i disini 1 }
for j:=1 to kolom do { j disini 1 }
begin
for z:=1 to baris do { z disini 1 }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
Loop ketiga Z tahap pertama :
Matrik A[1,1] lihat tabel matrik A 1,1 elemenya bernilai ( 2 ), MatrkiB [1,1] lihat juga tabel matrik B elemenya ( 1 ), nilai matrikA(2) * matrikB(1) = 2
hasil [i,j] bernilai 0 nah ini akan di tambahkan dengan nilai 2 ( 0 + 2 = 2 ). hasil perkalian matrik A dan B pada lopp z (pertama ). dan nilainya disimpan sementara di hasil[i,j] tersimpan nilai 2.
loop Z tahap kedua :
for i:=1 to baris do { i disini 1 }
for j:=1 to kolom do { j disini 1 }
begin
for z:=1 to baris do { z disini 2 }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
Matrik A[1,2] lihat tabel matrikA 1,2 elemenya bernilai ( 3 ), MatrikB [2,1] lihat juga tabel matrik B elemenya ( 4 ), nilai matrikA(3) * matrikB(4) = 12
Maka nilai yang tersimpan sementara tadi 2 + 12 = 14 ( tersimpan sementara di memori )
Dan karena ini loop terakhir maka hasil[i,j] atau jika berdasarkan akses indeks maka hasil[1,1] = 14
Loop ketiga ( z ) berakhir maka loop kedua ( j ) naik satu tingkat lagi bernilai 2 dan loop ketiga dimulai lagi dari angka 1 :
for i:=1 to baris do { i disini 1 }
for j:=1 to kolom do { j disini 2 }
begin
for z:=1 to baris do { z disini 1 }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
Matrik A[1,1] lihat tabel matrik A 1,1 elemenya bernilai ( 2 ), MatrkiB [1,2] lihat juga tabel matrik B elemenya ( 3 ), nilai matrikA(2) * matrikB(3) = 6
hasil [i,j] bernilai 0 nah ini akan di tambahkan dengan nilai 6 ( 0 + 6 = 6 ). hasil perkalian matrik A dan B pada lopp z (pertama ). dan nilainya disimpan sementara di hasil[i,j] tersimpan nilai 6.
loop Z tahap kedua :
for i:=1 to baris do { i disini 1 }
for j:=1 to kolom do { j disini 2 }
begin
for z:=1 to baris do { z disini 2 }
hasil[i,j] := hasil[i,j] + matrikA[i,z] * matrikB[z,j];
end;
Matrik A[1,2] lihat tabel matrikA 1,2 elemenya bernilai ( 3 ), MatrikB [2,2] lihat juga tabel matrik B elemenya ( 2 ), nilai matrikA(3) * matrikB(2) = 6
Maka nilai yang tersimpan sementara tadi 6 + 6 = 12 ( tersimpan sementara di memori )
Dan karena ini loop terakhir maka hasil[i,j] atau jika berdasarkan akses indeks maka hasil[1,2] = 12
Dan ketika loop kedua habis di eksekusi loop paling luar akan naik tingkat lagi yang tadinya i bernilai ( 1 ) akan bernilai ( 2 ) itu artinya loop akan berpindah baris.
Dan proses akan terulang seperti awal lagi terus menerus sampai hasilnya akan seperti gambar di bawah ini jika program di runing :
 |
| Gambar 15 : hasil program perkalian matrik diatas |
5. Operasi Perkalian Matrik X Vektor
Perkalian matrik dengan vektor adalah perkalian N * N, simpelnya jika matrik A x B maka jumlah kolom matrik B harus sama dengan jumlah baris matrik A .
Agar lebih hemat waktu silahkan lihat gambar 16 di bawah ini :
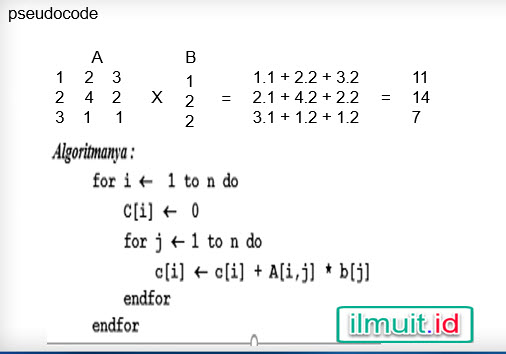 |
Gamabar 16 : Operasi Perkalian Matrik X Vektor pascal |
Jumlah kolom matrik B harus sama dengn jumlah baris matrik A .
Agar lebih memahami silahkan lihat source code di bawah ini agar lebih paham dan jelas :
program matrikXvektor;
uses crt;
type
dataM = array[1..10,1..10] of integer;
dataV = array[1..10] of integer;
var
matrik : dataM;
vektor : dataV;
baris : integer;
procedure isimatrik;
var i,j : integer;
begin
write ('Ukuran Matriks (a x a) : '); readln(baris);
writeln;
writeln ('Matrik =');
writeln;
for i:=1 to baris do
begin
for j :=1 to baris do
begin
gotoxy (j*5,i+8);
read(matrik[i,j]);
end;
end;
writeln;
writeln('Vektor =');
writeln;
for i:=1 to baris do
begin
readln(vektor[i]);
end;
end;
procedure perkalian(m1:dataM; m2:dataV; baris:integer);
var hasil : dataV;
i,j : integer;
begin
for i:=1 to baris do
begin
hasil[i]:= 0 ;
for j:=1 to baris do
begin
hasil[i]:= hasil[i] + m1[i,j] * m2[j];
end;
end;
writeln;
writeln('Output : A . B = ');
for i:= 1 to baris do
begin
writeln(hasil[i]);
writeln;
end;
readln;
end;
begin
clrscr;
writeln;
writeln;
isimatrik;
perkalian(matrik,vektor,baris);
readln;
end.
uses crt;
type
dataM = array[1..10,1..10] of integer;
dataV = array[1..10] of integer;
var
matrik : dataM;
vektor : dataV;
baris : integer;
procedure isimatrik;
var i,j : integer;
begin
write ('Ukuran Matriks (a x a) : '); readln(baris);
writeln;
writeln ('Matrik =');
writeln;
for i:=1 to baris do
begin
for j :=1 to baris do
begin
gotoxy (j*5,i+8);
read(matrik[i,j]);
end;
end;
writeln;
writeln('Vektor =');
writeln;
for i:=1 to baris do
begin
readln(vektor[i]);
end;
end;
procedure perkalian(m1:dataM; m2:dataV; baris:integer);
var hasil : dataV;
i,j : integer;
begin
for i:=1 to baris do
begin
hasil[i]:= 0 ;
for j:=1 to baris do
begin
hasil[i]:= hasil[i] + m1[i,j] * m2[j];
end;
end;
writeln;
writeln('Output : A . B = ');
for i:= 1 to baris do
begin
writeln(hasil[i]);
writeln;
end;
readln;
end;
begin
clrscr;
writeln;
writeln;
isimatrik;
perkalian(matrik,vektor,baris);
readln;
end.
Hasil program diatas adalah siperti tampak gambar di bawah ini :
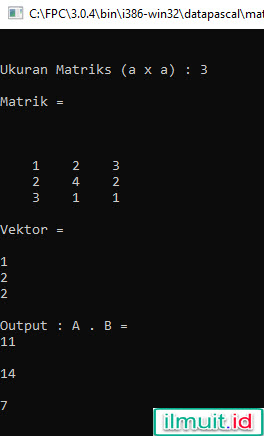 |
| Gambar 17 :hasil perkalian matrik x vektor pascal |
Baca Juga : Algoritma 2 : Pengertian Procedure Dan Penerapan Dalam Bahasa Pascal
Nah pembahasan kita tentang array matrik dan operasi perkalian, penjumlahan , pengurangan matrik serta perkalian matrik x vektor sampai disini pembahasanya tetaplah belajar sampai ilmu itu bisa berbicara dengan anda karena ilmu itu memilih tempat, bukan anda yang memilihnya luruskan niat anda dengan benar untuk mencari ilmu - ilmuit.id



Post a Comment for "Algoritma 2 : Array Dua Dimensi Beserta Contoh Program Pascal"